[cs231n] lec14 - Reinforcement Learning

이전 강의

• Supervised Learning (Classification)
• Unsupervised Learning (GAN ...)

 

• Reinforcement Learning: agent의 보상을 최대화할 수 있는 행동이 무엇인지 학습
• Agent: 환경(enviroment)에서 행위(action)를 하는 주체, 행위에 따라 보상(rewards)을 받는다.

 

---

 

Overview

• Reinforcement Learning?
• Markov Decision Precesses
• Q-Learning
• Policy Gradients

 

Reinforcement Learning

Reinforcement에는 agent, environment 존재

1. environment가 agent에게 state을 제공
2. agent가 action을 취함
3. 해당 action에 대해 environment가 reward와 next state 제공
4. 이를 environment가 terminal state을 줄 때까지 반복 ==> episode가 끝남

 

Example: 바둑

 

Markov Decision Process

• MDP로 RL problem을 수식화 할수 있음
• MDP는 Markov property를 만족한다.

*Markov Property 현재 상태만으로 전체 상태를 나타내는 성질

• S: 가능한 상태들의 집함
• A: 가능한 action들의 집합
• R: (state, action) 쌍을 보상으로 매핑하는 함수
• P: 전이 확률(transition probability), (state, action) 쌍이 주어졌을때 전이될 다음 상태에 대한 분포
• gamma: discount factor, 현재 보상과 나중의 보상에 대한 가중치 정도 how much we value rewards coming up soon versus later on

 

MDP 작동 방식

1. 초기 (t=0): environment가 초기 state을 샘플링 => S-0
2. t=0 ~ terminal state: 아래 과정 반복
3. agent가 action을 선택 => A_t
4. environment가 (S_t, A_t)에 대해 reward 샘플링 & next state 샘플링 => R_t, S_t+1
5. agent가 R_t, S_t+1을 받음

 

• policy pi : 각 state에서 agent가 어떤 action을 취할지 명시하는 함수 (S->A)
• policy: stochastic / deteministic
• 목표 'commulative discounted reward를 최대화하는 pi_*를 찾는 것'

(future reward도 포함된다. discount factor 적용)

 

A simple MDP: Grid World

목표: 최소한의 action으로 회색 영역에 도달하는 것

• state: 각 칸
• action: 상, 하, 좌, 우 이동
• reward: 매 이동마다 R = -1

 

1. MDP 정하기

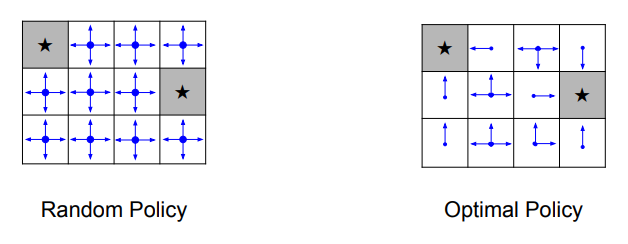
• Random policy

이동 방향을 랜덤하게 정하는 방법. 모든 방향이 동일한 확률을 가짐

• Optimal policy

점점 terminal state에 가까워지도록 만드는 action을 선택.

 

2. Optimal policy Pi*

reward의 총 합을 최대화하는 optimal policy pi*를 찾아야 한다. 

 

Q) MDP의 randomness를 어떻게 처리할지? (초기 state 샘플링할 때, transition probability 분포에서 next state을 샘플링할 때 randomness)

A) reward의 총합의 기댓값을 최대화

 

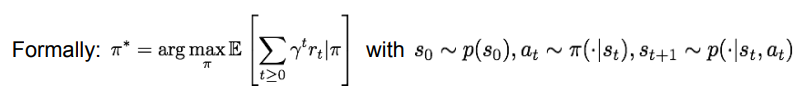
• pi* = policy pi에 대한 future reward의 합의 기댓값을 최대화시키는 것
• 초기상태: state 분포를 따름
• action: 어떤 state이 주어졌을 때 policy가 가지는 분포로부터 샘플링
• next state: 전이 확률 분포에서 샘플링

 

Definition: Value function and Q-value function

• Value function

state S에 대한 policy가 주어졌을때 누적 보상에 대한 기댓값 (현재 state가 얼마나 좋은 것인지)

• Q-value function

policy PI, action A, state S가 주어졌을때 받을 수 있는 누적 보상의 기댓값 (해당 state에서 어떤 action을 취하는게 좋은지)

 

Bellman equation

• 최적의 Q-value function (Q*)은 주어진 (state, action) 쌍에서 얻을 수 있는 누적 보상의 기댓값을 최대화한다. 
• Q*는 Bellman equation을 따른다. 

(12:50부터)